Keep your order, stupid!
Have you ever wondered how collections in Scala treat their internal order? I’ll freely admit – the above problem has never given me sleepless nights (to put it mildly). What’s sorted is sorted. It doesn’t matter if it’s a collection or a list, does it?
…
Well, not really.
Some time ago, I had to deal with a very interesting case that even bypassed a quite sensible sieve of tests. As usual, however, the devil is in the detail. And these “details” in the case of Scala are quite a lot (which, incidentally, is the flywheel of the opponents of this language). To the point, however, take a look at the model below:
case class Student(id: String, firstName: String, lastName: String, age: Int, avgGrades: Double)
case class Course(name: String, enrolledStudents: Set[Student], reserveList: Set[Student])
We have a class reflecting the student and the course they can be enrolled in or go on the reserve list. Now let’s try to implement the following contract:
def createBasedOnGrade(name: String, students: List[Student], maxPositions: Int): Course
We want to be able to create a new course with a maximum number of places (maxPositions), where the average grade (avgGrades) decides whether a student is enrolled or placed on the reserve list. This behaviour can be achieved very simply in Scala using the sortBy and splitAt functions (note, we sort in descending order!)
val (eligible, notEligible) = students
.sortBy(_.avgGrades)(Ordering[Double].reverse)
.splitAt(maxPositions)
Course(name, eligible, notEligible)
The code is correct, with type accuracy, which the compiler hints at quite quickly. The collections in Course are Sets, and we are operating on lists. This can be easily fixed, however, how will it be most elegant?
Course(name, eligible.toSet, notEligible.toSet)
A bit ugly, let’s try to do the conversions to the set a bit higher up
val (eligible, notEligible) = students
.toSet
.sortBy(_.avgGrades)(Ordering[Double].reverse)
Won’t pass, after all on a collection we don’t do a toSet, silly me!
val (eligible, notEligible) = students
.sortBy(_.avgGrades)(Ordering[Double].reverse)
.toSet
.splitAt(maxPositions)
Well, now it’s elegant. The kodziah looks nice and seems to meet our requirements. “Seems”, however, is not enough if you are a self-respecting engineer. You need to write a test.
it should “create a course with enrolled and reserve list” in {
val students = List(
Student(“id1”, “John”, “Newman”, 20, 4.3),
Student(“id2”, “Mark”, “James”, 21, 4.8),
Student(“id3”, “Olivia”, “Spencer”, 23, 4.75),
Student(“id4”, “Natalie”, “Smith”, 19, 4.2)
)
val course = Course.createBasedOnGrade(“Mathematical analysis”, students, maxPositions = 2)
course.enrolledStudents.map(_.id) should contain only (“id2”, “id3”)
course.reserveList.map(_.id) should contain only (“id1”, “id4”)
}
The test no longer seems to leave any illusions. We have sifted out the “weak” students, and the best ones can be enrolled in an upgraduated course. Let’s assume that we go out into production with such code. Probably not an hour would have passed and already the phones would be ringing off the hook in the dean’s office with complaints from annoyed students. “How come that stupid Ann got into the course and I didn’t. After all, I have a higher average!”
As I mentioned at the beginning of this text, the devil is in the details. The details in this case are two. The first is the location of the toSet conversion, which occurs after sorting and before dividing students based on average. This conversion does not create a sorted set, so we lose the information available in the previous step. However, why is the test unable to detect this. Were we ‘lucky’, and by creating a set based on the list we got the order we wanted?
The solution is even more subtle, as the debugger beautifully shows us.
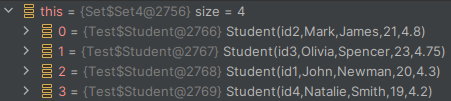
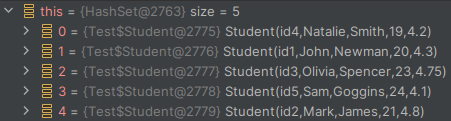
In the case of the first test, our collection has the type Set$Set4, while in the second it is the slightly more familiar HashSet. What is this mysterious Set4? Well, it is one of the many optimisations brought about by the language itself – a simplified implementation of a set, where its elements are nothing more than the fields of a class:
final class Set4[A] private[collection] (elem1: A, elem2: A, elem3: A, elem4: A)
In Scala, there are simplified types for collections: one-, two-, three- and four-element collections. When such a set is created, the elements do not go to random places, but are assigned sequentially to fields. To show an error in the test, simply increase the list of students in the test from four to five.
The puzzle is solved. You can go on your way.