Trzymaj swój porządek, głupcze!
Czy zastanawialiście się kiedyś, w jaki sposób kolekcje w Scali traktują swój wewnętrzny porządek? Przyznam się bez bicia – powyższy problem nigdy nie spędzał mi snu z powiek (delikatnie mówiąc). Co posortowane, to posortowane. Nieważne czy to zbiór, czy lista, prawda?
…
No nie za bardzo.
Jakiś czas temu miałem do czynienia z bardzo ciekawym przypadkiem, który ominął nawet całkiem sensowne sito testów. Diabeł jednak jak zwykle tkwi w szczegółach. A tych “szczegółów” w przypadku Scali jest całkiem sporo (co notabene jest kołem zamachowym przeciwników tego języka). Do rzeczy jednak, spójrz na poniższy model:
case class Student(id: String, firstName: String, lastName: String, age: Int, avgGrades: Double)
case class Course(name: String, enrolledStudents: Set[Student], reserveList: Set[Student])
Mamy klasę odzwierciedlającą studenta oraz kurs, na który może być on zapisany bądź trafić na listę rezerwową. Spróbujmy teraz zaimplementować następujący kontrakt:
def createBasedOnGrade(name: String, students: List[Student], maxPositions: Int): Course
Chcemy mieć możliwość utworzenia nowego kursu z limitem miejsc (maxPositions), gdzie o zapisie bądź trafieniu na listę rezerwową zadecyduje średnia ocen (avgGrades). Takie zachowanie możemy osiągnać w Scali bardzo prosto za pomocą funkcji sortBy oraz splitAt (uwaga, sortujemy malejąco!)
val (eligible, notEligible) = students
.sortBy(_.avgGrades)(Ordering[Double].reverse)
.splitAt(maxPositions)
Course(name, eligible, notEligible)
Kod jest poprawny, z dokładnością do typów, co kompilator dosyć szybko nad podpowie. Kolekcje w Course to Set’y, a my operujemy na listach. Da się to jednak łatwo naprawić, jak jednak będzie najładniej?
Course(name, eligible.toSet, notEligible.toSet)
Troche brzydkie, spróbujmy wykonać konwersje do zbioru nieco wyżej
val (eligible, notEligible) = students
.toSet
.sortBy(_.avgGrades)(Ordering[Double].reverse)
Nie przejdzie, przecież na zbiorze nie zrobimy toSet, głupi ja!
val (eligible, notEligible) = students
.sortBy(_.avgGrades)(Ordering[Double].reverse)
.toSet
.splitAt(maxPositions)
No, teraz jest elegancko. Kodziaszek wygląda ładnie i wydaje się, że spełnia nasze wymagania. “Wydaje się”, to jednak za mało jeśli jest się szanującym się inżynierem. Trzeba napisać test.
it should “create a course with enrolled and reserve list” in {
val students = List(
Student(“id1”, “John”, “Newman”, 20, 4.3),
Student(“id2”, “Mark”, “James”, 21, 4.8),
Student(“id3”, “Olivia”, “Spencer”, 23, 4.75),
Student(“id4”, “Natalie”, “Smith”, 19, 4.2)
)
val course = Course.createBasedOnGrade(“Mathematical analysis”, students, maxPositions = 2)
course.enrolledStudents.map(_.id) should contain only (“id2”, “id3”)
course.reserveList.map(_.id) should contain only (“id1”, “id4”)
}
Test już chyba nie pozostawia złudzeń. Odsialiśmy “słabych” studenciaków, a najlepsi mogą zostać zapisani na upgragniony kurs. Założmy, że wychodzimy z takim kodem na produkcję. Pewnie nie minęłaby godzina, a już w dziekanacie rozdzwoniłyby się telefony z pretensjami od wkurzonych żaków. “Jak to możliwe, że ta głupia Anka dostała się na kurs, a ja nie. Przecież mam wyższą średnią!”
Jak wspomniałem na początku tego tekstu, diabeł tkwi w szczegółach. Szczegóły w tym przypadku są dwa. Pierwszy z nich, to umiejscowienie konwersji toSet, która następuje po sortowaniu, a przed podziałem na studentów w oparciu o średnią. Konwersja ta nie tworzy zbioru posortowanego, tracimy więc informację, dostępną w poprzednim kroku. Dlaczego jednak test nie jest w stanie tego wykryć. Czy mieliśmy “farta”, i tworząc zbiór na podstawie listy otrzymaliśmy żądaną przez nas kolejność?
Rozwiązanie jest jeszcze bardziej subtelne, co pięknie pokazuje nam debugger.
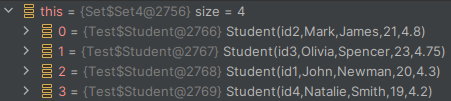
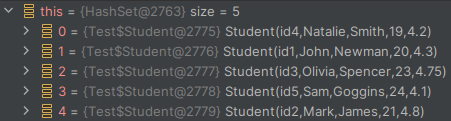
W przypadku pierwszego testu, nasz zbior legitymizuje się typem Set$Set4, w drugim zaś jest to już nieco bardziej znany HashSet. Czymże jest ten tajemniczy Set4? Ano jest to jedna z wielu optymalizacji, jaką niesie ze sobą sam język – uproszczona implementacja zbioru, gdzie jego elementy nie są niczym innym, jak tylko polami klasy:
final class Set4[A] private[collection] (elem1: A, elem2: A, elem3: A, elem4: A)
W Scali istnieją uproszczone typy dla zbiorów: jedno, dwu, trzy i czteroelementowego. W chwili tworzenia takiego zbioru elementy nie trafiają na przypadkowe miejsca, lecz są przypisywane kolejno do pól. Aby wykazać błąd w teście, wystarczy zwiększyć listę studentów w teście z czterech do pięciu.
Zagadka rozwiązana. Można się rozejść.